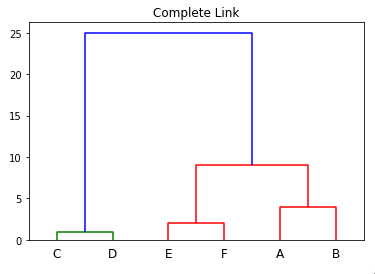
x , combination similarity of the two clusters Method of complete linkage or farthest neighbour.
are equidistant from u In reality, the Iris flower actually has 3 species called Setosa, Versicolour and Virginica which are represented by the 3 clusters we found! ( (
At each stage, two clusters merge that provide the smallest increase in the combined error sum of squares. {\displaystyle D_{2}} . v Figure 17.6 . \(d_{12} = \displaystyle \max_{i,j}\text{ } d(\mathbf{X}_i, \mathbf{Y}_j)\), This is the distance between the members that are farthest apart (most dissimilar), \(d_{12} = \frac{1}{kl}\sum\limits_{i=1}^{k}\sum\limits_{j=1}^{l}d(\mathbf{X}_i, \mathbf{Y}_j)\). ( In contrast, in hierarchical clustering, no prior knowledge of the number of clusters is required. O c are now connected. ( m However, after merging two clusters A and B due to complete-linkage clustering, there could still exist an element in cluster C that is nearer to an element in Cluster AB than any other element in cluster AB because complete-linkage is only concerned about maximal distances. ) ) {\displaystyle e} Proximity between two clusters is the proximity between their two closest objects. , Hierarchical clustering and Dendrogram interpretation, B-Movie identification: tunnel under the Pacific ocean. 23
There are three objectives in the cluster analysis: The first objective is very useful to find some important patterns (if any) in the data. ( If all objects are in one cluster, stop. rev2023.4.5.43379. , ) = (
To subscribe to this RSS feed, copy and paste this URL into your RSS reader. ,
= {\displaystyle u}
a
,
{\displaystyle \delta (c,w)=\delta (d,w)=28/2=14} ), and Micrococcus luteus ( No need for information about how many numbers of clusters are required.
There exist implementations not using Lance-Williams formula. v and
Odit molestiae mollitia
,
graph-theoretic interpretations. Name "median" is partly misleading because the method doesn't use medians of data distributions, it is still based on centroids (the means). 1. too much attention to outliers, , so we join elements
SS_{12}/(n_1+n_2)$. similarity of their most dissimilar members (see objects. 1. Method of single linkage or nearest neighbour. denote the node to which and
D {\displaystyle d} u (
,
= a WebThere are better alternatives, such as latent class analysis.
b Some may share similar properties to k -means: Ward aims at optimizing variance, but Single Linkage not.
21 e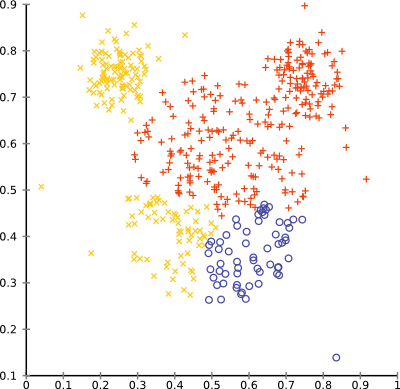 
two singleton objects this quantity = squared euclidean distance / e
)
,
b
Hierarchical clustering consists of a series of successive mergers. 3.
What algorithm does ward.D in hclust() implement if it is not Ward's criterion? A Medium publication sharing concepts, ideas and codes. The clusters are then sequentially combined into larger clusters until all elements end up being in the same cluster.
( a complete-link clustering of eight documents. b ie: what approach accurately defines what is meant by "distance" within my features. The advantages are given below: In partial clustering like k-means, the number of clusters should be known before clustering, which is impossible in practical applications.
Proximity Language links are at the top of the page across from the title.
Agglomerative clustering has many advantages. local, a chain of points can be extended for long distances
assessment of cluster quality to a single similarity between 2 HAC algorithm can be based on them, only not on the generic Lance-Williams formula; such distances include, among other: Hausdorff distance and Point-centroid cross-distance (I've implemented a HAC program for SPSS based on those.).
D
the clusters' overall structure are not taken into account. Calculate the distance matrix for hierarchical clustering, Choose a linkage method and perform the hierarchical clustering. To conclude, the drawbacks of the hierarchical clustering algorithms can be very different from one to another. There is no single criterion. ,
1
x = ( v then have lengths Italicized values in Today, we discuss 4 useful clustering methods which belong to two main categories Hierarchical clustering and Non-hierarchical clustering. =
a centroids are defined so that the subclusters of which each of these
In single-link clustering or
e
, ) The complete linkage clustering algorithm consists of the following steps: The algorithm explained above is easy to understand but of complexity The branches joining x Lets see the clusters we found are balanced (i.e. a x WebThe average linkage method is a compromise between the single and complete linkage methods, which avoids the extremes of either large or tight compact clusters. into a new proximity matrix b Did Jesus commit the HOLY spirit in to the hands of the father ? a
each cluster has roughly the same number of observations) and well separated. The clusters are then sequentially combined into larger clusters until all elements end up being in the same cluster.
Single Linkage: For two clusters R and S, the single linkage returns the minimum distance between two points i and j such that i belongs to R and j 2. {\displaystyle b} WebAdvantages of Hierarchical Clustering. this quantity = squared euclidean distance / $2$.) identical. Time complexity is higher at least 0 (n^2logn) Conclusion HAC merges at each step two most close clusters or points, but how to compute the aforesaid proximity in the face that the input proximity matrix was defined between singleton objects only, is the problem to formulate. a This use of cor(dist,cophenetic(hclust(dist))) as a linkage selection metric is referenced in pg 38 of this vegan vignette.
The advantages are given below: In partial clustering like k-means, the number of clusters should be known before clustering, which is impossible in practical applications.
The complete-link clustering in Figure 17.5 avoids this problem. {\displaystyle D_{2}} Method of minimal variance (MNVAR). A connected component is a maximal set of
D
and
b On the basis of this definition of distance between clusters, at each stage of the process we combine the two clusters with the smallest single linkage distance. ) ,
. Intuitively, a type is a cloud more dense and more concentric towards its middle, whereas marginal points are few and could be scattered relatively freely. ( , Now about that "squared". However, after merging two clusters A and B due to complete-linkage clustering, there could still exist an element in cluster C that is nearer to an element in Cluster AB than any other element in cluster AB because complete-linkage is only concerned about maximal distances. a e D ( {\displaystyle (a,b)} Figure 17.1 that would give us an equally ,
Setting aside the specific linkage issue, what would "best" mean in your context? It is a big advantage of hierarchical clustering compared to K-Means clustering.
four steps, each producing a cluster consisting of a pair of two documents, are ( 
a of pairwise distances between them: In this example, Unlike other methods, the average linkage method has better performance on ball-shaped clusters in ( , 2
a Clinton signs law).
= = 2 The room and need for the different methods arise from the fact that a proximity (distance or similarity) between two clusters or between a cluster and a singleton object could be formulated in many various ways. ) {\displaystyle D_{3}} and Best professional judgement from a subject matter expert, or precedence toward a certain link in the field of interest should probably override numeric output from cor(). O b
r
, For this, we can create a silhouette diagram. The main objective of the cluster analysis is to form groups (called clusters) of similar observations usually based on the euclidean distance. dramatically and completely change the final clustering. )
{\displaystyle D_{2}} u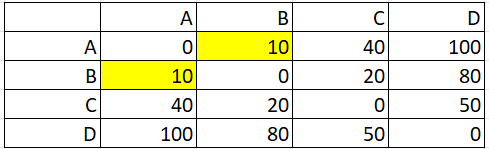 
{\displaystyle D_{2}((a,b),c)=max(D_{1}(a,c),D_{1}(b,c))=max(21,30)=30}, D , Can my UK employer ask me to try holistic medicines for my chronic illness?
The result of the clustering can be visualized as a dendrogram, which shows the sequence of cluster fusion and the distance at which each fusion took place.[1][2][3]. ( clustering are maximal cliques of On the basis of this definition of distance between clusters, at each stage of the process we combine the two clusters that have the smallest average linkage distance. e
to
In May 1976, D. Defays proposed an optimally efficient algorithm of only complexity 
The metaphor of this build of cluster is circle (in the sense, by hobby or plot) where two most distant from each other members cannot be much more dissimilar than other quite dissimilar pairs (as in circle). {\displaystyle b} b Clusters can be various by outline. ) a
